Write an Absolute Value Equation That Has the Solutions X=8 and X=18.

Learn How to Solve Absolute Value Equations in 3 Easy Steps!

The following step-by-step guide will show you how to solve absolute value equations and absolute value functions with ease (Algebra)

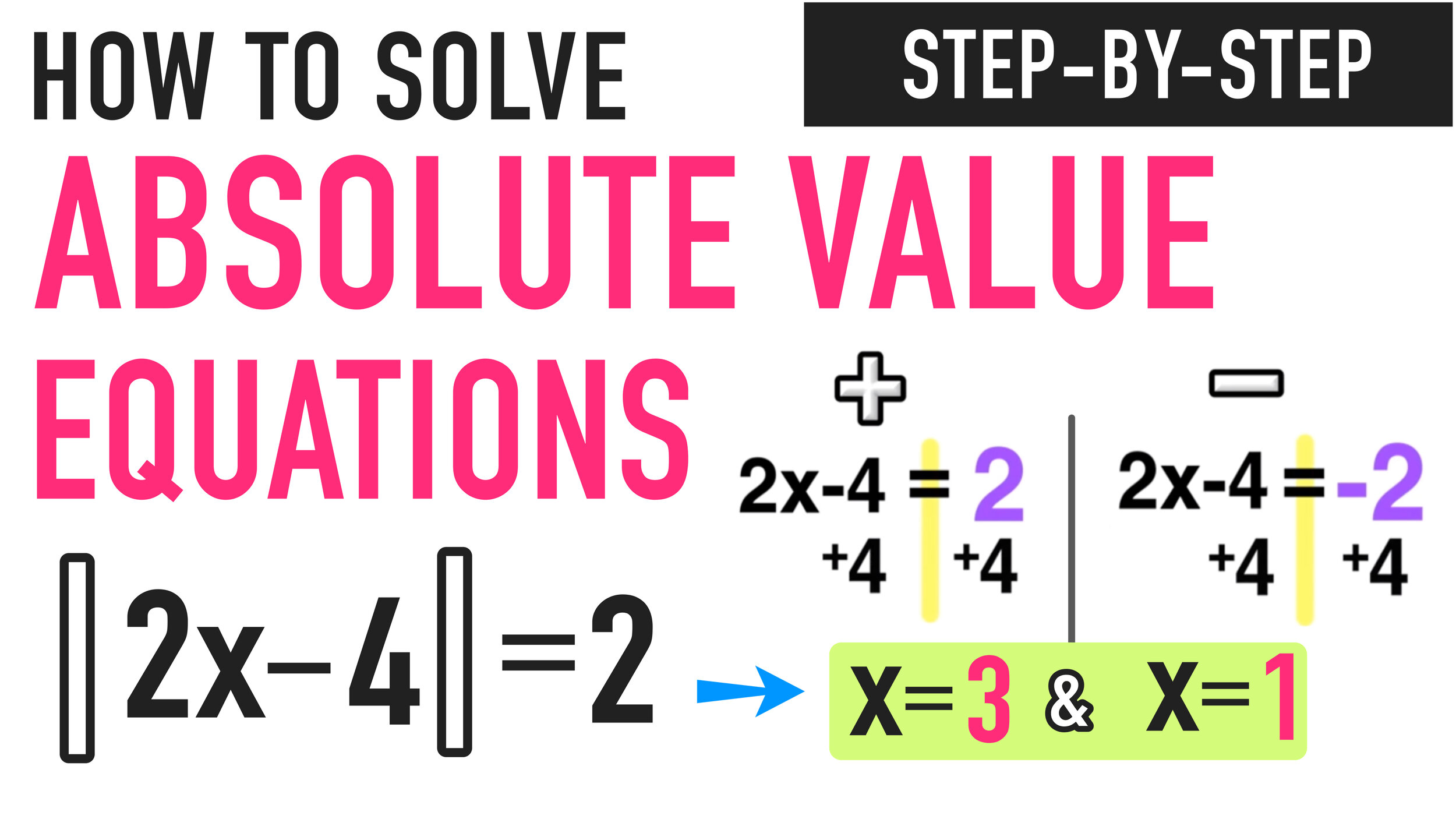
Welcome to this free lesson guide that accompanies this Solving Absolute Value Equations Tutorial where you will learn the answers to the following key questions and information:

• How to solve an absolute value equation

• How to solve an absolute value function

• How to find both solutions to an absolute value equation

• Why is absolute value always positive?

This Complete Guide to Solving Absolute Value Equations includes several examples, a step-by-step tutorial and an animated video tutorial.

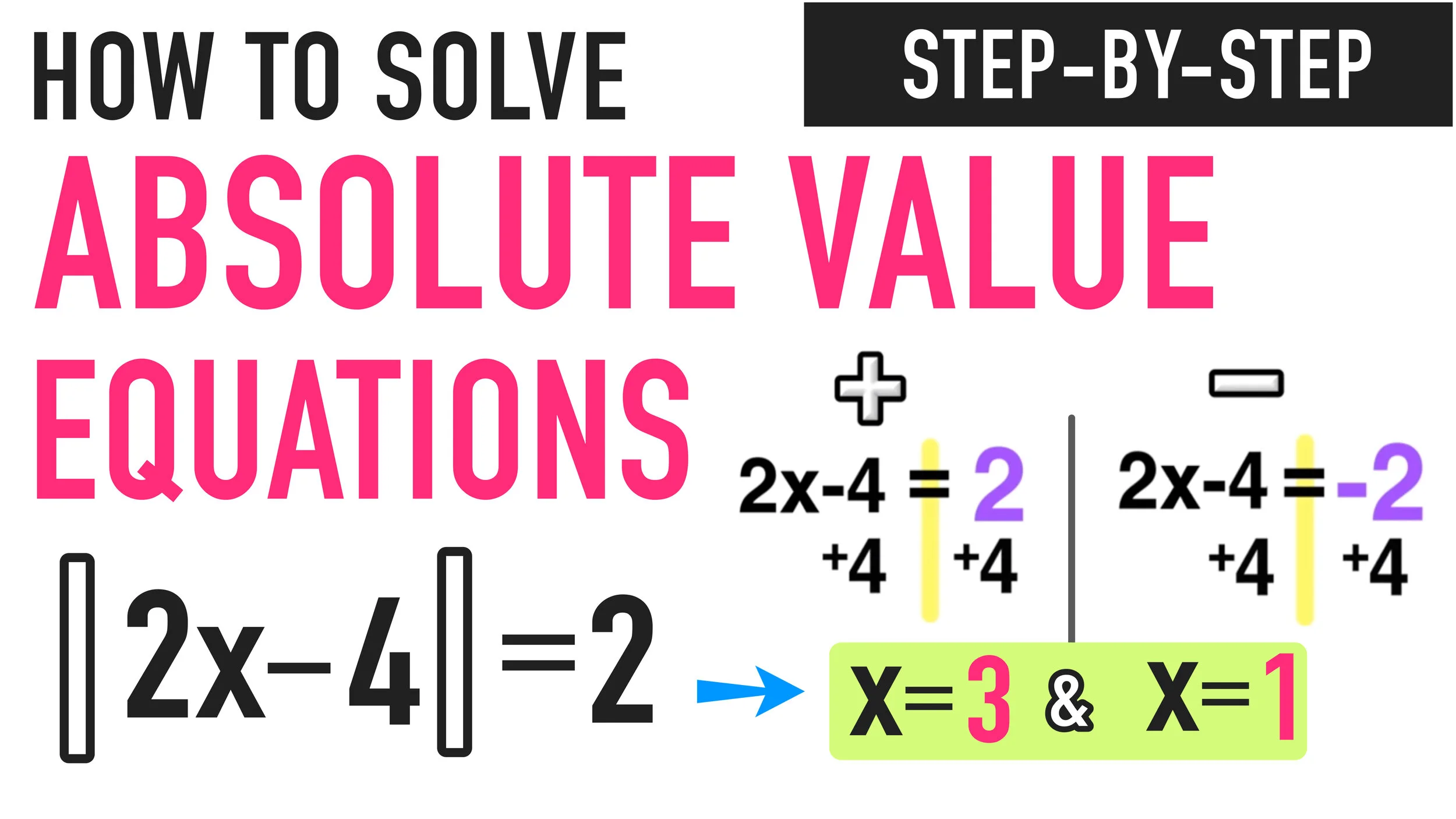
Intro to Solving Absolute Value Equations

Before you work on a few absolute value equations examples, let's quickly review some important information:

Fact: Any value inside of absolute value bars represents either a positive number or zero.

Notice that the absolute value graph in Figure 1 has a range of y is greater than or equal to 0 (it is never negative)

Figure 1: The parent function for absolute value.

Furthermore, consider the example below:

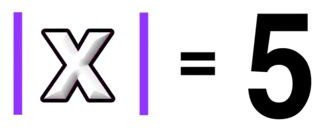
There are two values that would make this equation true!

The absolute value of 5 AND the absolute value of -5 both equal positive 5.

This should make sense when you graph the line y=5 over the absolute value function graph because you can see that there are two intersection points, and thus two solutions.

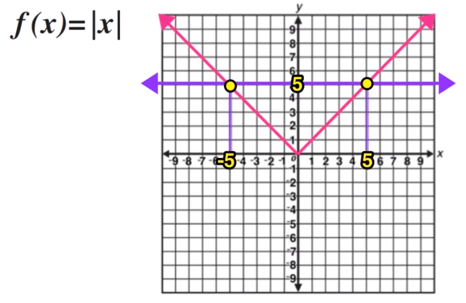
Absolute value functions can have up to two solutions!

Now you know that ABSOLUTE VALUE EQUATIONS CAN HAVE TWO SOLUTIONS.

Now you are ready to try a few examples.

Solving Absolute Value Equations Example #1

We will be using the following 3-step process that can be used to solve any absolute value equation:

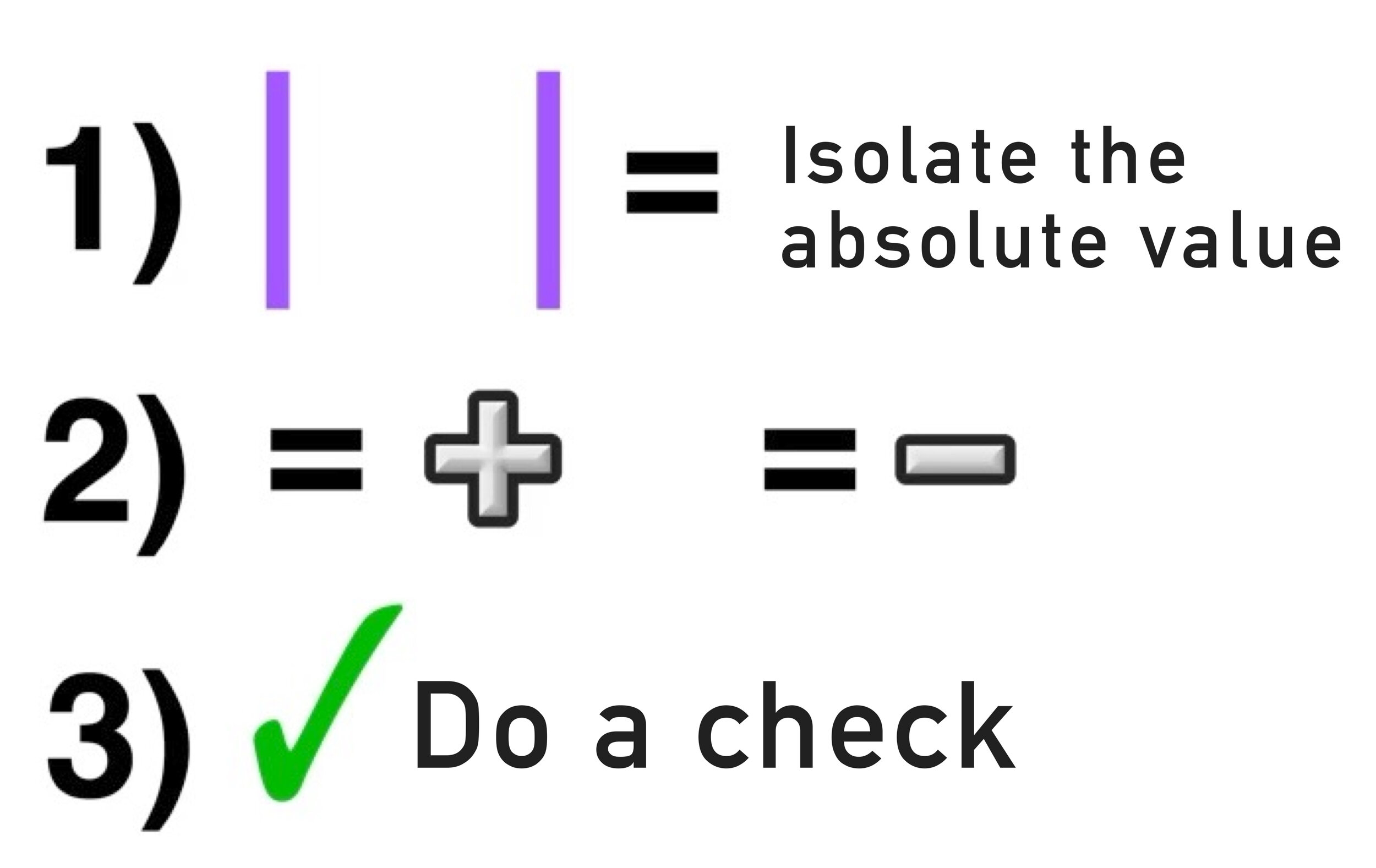
STEP ONE: Isolate the Absolute Value

In this example, the absolute value is already isolated on one side of the equals sign, which means that there are no other terms outside of the absolute value, so you can move onto step two.

STEP TWO: Solve for Positive AND Solve for Negative

For step two, you have to take the original equation |x+3| = 6 and split it up into two equations, one equal to POSITIVE 6 and the other equal to NEGATIVE 6. You also get rid of the absolute value bars.

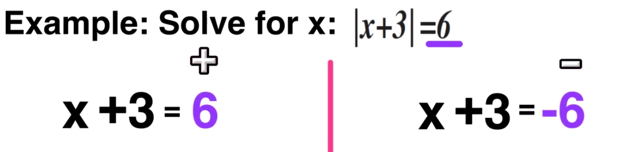
Set up two equations (positive and negative) and ditch the absolute value bars.

Now you just have to solve each equation for x as follows:

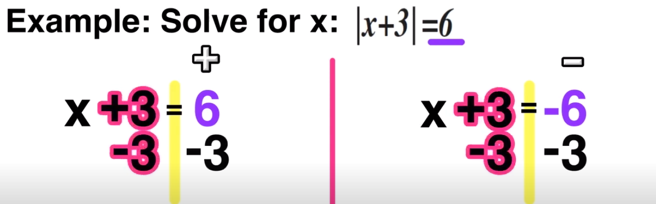
And now you have concluded that there are two solutions to |x+3|=6, x=3 and x=-9.

STEP THREE: Check Your Answer

Finally, do a quick check by plugging both answers into the original equation, |x+3|=6, to make sure that they are correct:

Left: replace x with 3. Right: replace x with -9

Both equations are true.

Since the checks worked out, you can conclude that:

Final Answer: The solutions to |x+3|=6 are x=3 and x=-9

Solving Absolute Value Equations Example #2

Again, you will follow the three-step process to solving this absolute value equation:

STEP ONE: Isolate the Absolute Value

Unlike the last example, the absolute value is not already isolated on one side of the equal sign, because there is a +8 outside of it that needs to be moved to the other side as follows:

Step One: Isolate the absolute value!

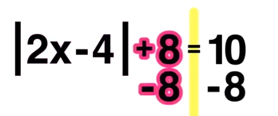
Now the absolute value is isolated.

Now that you have isolated the absolute value on one side of the equal sign, you are ready for the next step.

STEP TWO: Solve for Positive AND Solve for Negative

The next step is to ditch the absolute value bars and solve the following equations:

Positive: 2x-4=2 and Negative: 2x-4=-2

Now you have TWO solutions: x=3 and x=1

STEP THREE: Check Your Answer

The final step is to plug both solutions, x=3 and x=1, into the original equation |2x-4|+8=10 and verify that each solution checks out and you are finished!

Go ahead and check the solution to Example 2 on your own! Did it work out?

Still Confused?

Check out this animated video tutorial on solving absolute value equations!

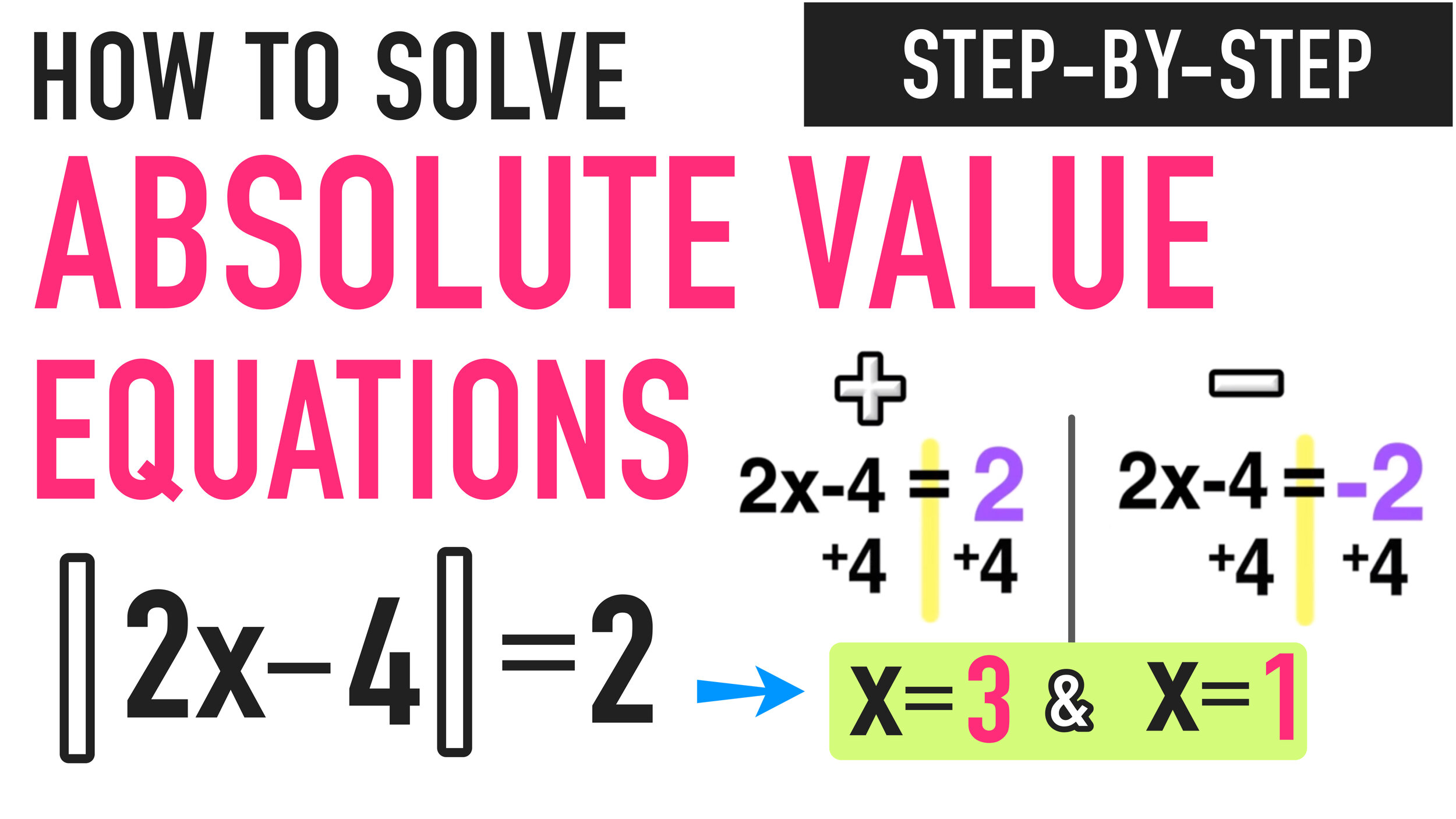
Looking for more practice with absolute value?

Check out the following free cube root resources:

Free Tutorial

Comment

Write an Absolute Value Equation That Has the Solutions X=8 and X=18.

Source: https://www.mashupmath.com/blog/solving-absolute-value-equations

Share this post